Question 1:
Diagram below shows a type of organelle found in muscle cells.
A biochemical reaction occurs in the organelle.
(b) The biochemical reaction that occurs in this organelle is summarized as follows:
(c) State two differences on the biochemical reaction occurring between muscle cell and yeast cell in the absence of gas R. [2 marks]
Answer:
(a)(i)
Mitochondrion
(a)(ii)
Membrane W is in the form of numerous folded layers to increase total surface area, for the efficiency of cellular respiration.
(b)(i)
Gas R is oxygen
(b)(ii)
Product S is water
(b)(iii)
Muscle cells need a large number of mitochondrion as an energy ATP supply in order to oxidise glucose in aerobic respiration.
(b)(iv)
– If the blood sugar is lower than the normal range, less energy is produced.
– Pancreas secretes glucagon to convert glycogen to glucose.
– Cellular respiration occurs.
(c)
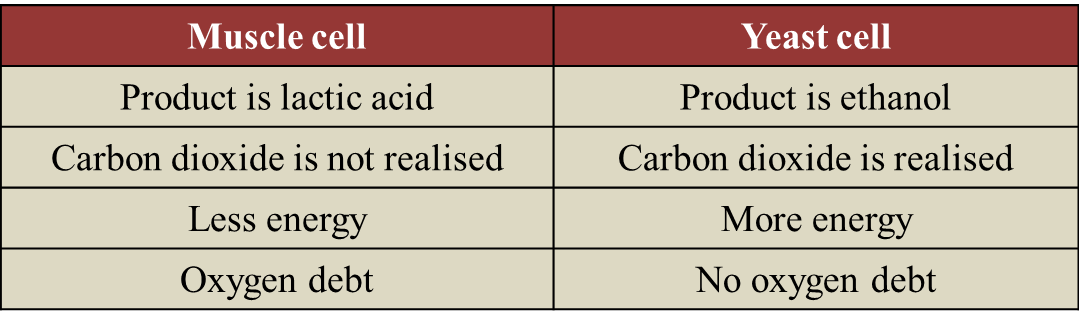
Diagram below shows a type of organelle found in muscle cells.
A biochemical reaction occurs in the organelle.
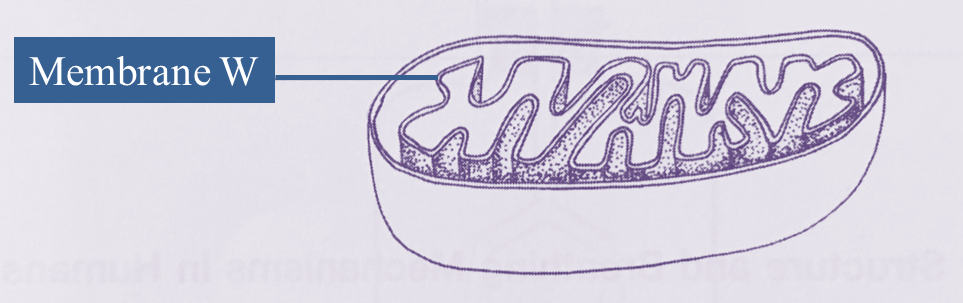
(a)(i) Name this organelle. [1 mark]
(ii) Explain why membrane W is in the form of numerous folded layers. [2 marks]
(b) The biochemical reaction that occurs in this organelle is summarized as follows:
 (i) Name gas R. [1 mark]
(i) Name gas R. [1 mark]
(ii) Name product S. [1 mark]
(iii) Explain why the muscle cell has a large number of these organelles. [2 marks]
(iv) If the blood sugar level is lower than the normal range, the biochemical reaction in this organelle can still occur.
Explain how. [3 marks]
(c) State two differences on the biochemical reaction occurring between muscle cell and yeast cell in the absence of gas R. [2 marks]
Answer:
(a)(i)
Mitochondrion
(a)(ii)
Membrane W is in the form of numerous folded layers to increase total surface area, for the efficiency of cellular respiration.
(b)(i)
Gas R is oxygen
(b)(ii)
Product S is water
(b)(iii)
Muscle cells need a large number of mitochondrion as an energy ATP supply in order to oxidise glucose in aerobic respiration.
(b)(iv)
– If the blood sugar is lower than the normal range, less energy is produced.
– Pancreas secretes glucagon to convert glycogen to glucose.
– Cellular respiration occurs.
(c)
